Specific Process Knowledge/Characterization/Profiler/Stylus profiler measurement uncertainty

Feedback to this page: click here

Stylus profiler measurement accuracy

The accuracy of a height measurement with the profiler depends on the measurement settings, the sample, the instrument calibration and the resolution.

Use the right measurement settings for your sample

Both the force setting and the scan speed are important: Too high force may compress a soft material like Al, Au or some polymers, while too low force may lead to the stylus "jumping" over features, especially if the scan speed is high. Too low scan speed may result in drift of the measurement and lots of noise while too high scan speed may mean that the stylus tip does not have time to reach the bottom of the features you are measuring (see the DektakXT manual, Figure 3 for details).

A sharp vertical step is easiest to measure. If the step is gradual or the surface is very rough, it can be difficult to determine where to measure and how the scan should be leveled.

Influence of calibration standard uncertainty

Figure 1: Measurement uncertainty from calibration uncertainty. Not to scale. How the linearity of the sensor means that measurement error increases approximately linearly with the size of the feature being measured. The percentage-wise error on the smallest standard step is larger than on the bigger standard step, so the lines are not totally straight.

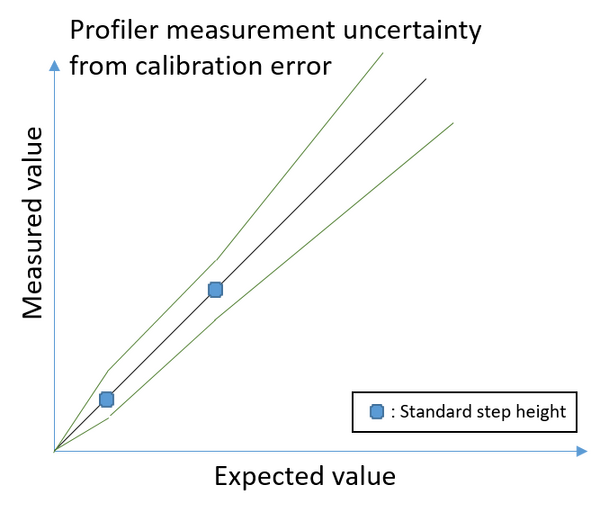
Nanolab staff check the instrument's measurement accuracy with a standard step height of 917 nm for the smaller ranges and 24.925 µm for the larger ranges, so that the middle ranges are checked with both standards. The 95 % confidence intervals for the standards are 17 nm for the 917 nm standard and 0.072 µm for the 24.925 µm standard. If the control measurement is beyond the limit set in our Quality Control procedure, the instrument is calibrated and the users informed (see LabManager for details, for instance the DektakXT control instruction and control measurement data)

All this means that the 95 % confidence interval of a 1 µm step measured with the smallest measurement range is at least the 1.8 % error of the standard step while the 95 % confidence interval of a 25 µm step measured with a larger range is at least the 0.3 % error of the standard step. Steps between 1 and 25 µm measured with the intermediate ranges will presumably have an intermediate error just due to the intrinsic uncertainty on the standard step height. See Figure 1.

Total uncertainty

Figure 2: The probability distributions of the main sources of error that are convoluted to create the total error on a profiler measurement.

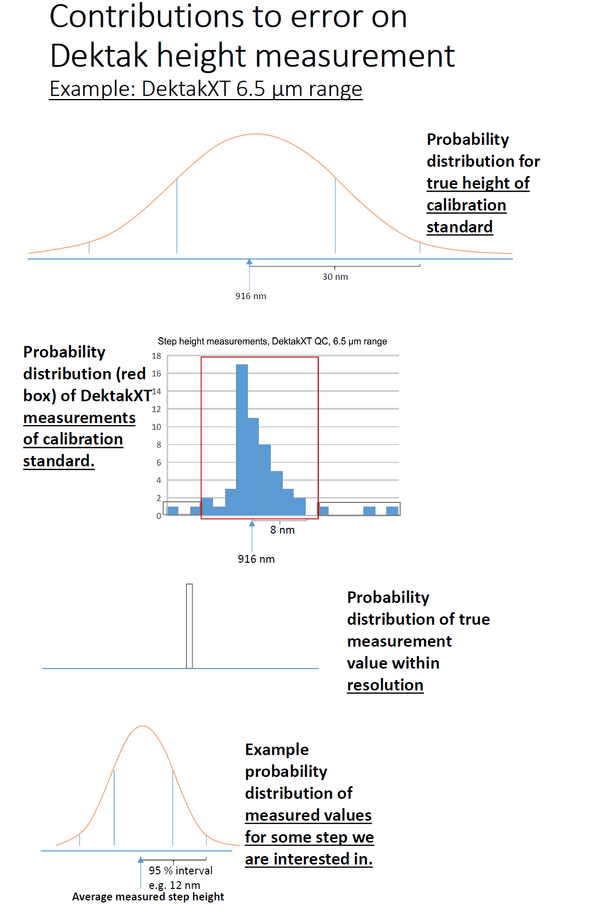
Apart from the error due to the standard step height's intrinsic uncertainty, there will be a contribution to the overall uncertainty from the deviation of the value that the profiler measures from the theoretical height of the standard step (since we accept some variation in our quality control routine, I call this QC error). In practice for the 917 nm standard this range is about ± 4 nm for the DektakXT and ± 8 nm for the P17, while for the large standard it ranges from about 0.06 µm on the DektakXT to about 0.15 µm on the P17.

There is also a tiny contribution to the total error from the instrument's limited resolution and finally of course there is random noise in any measurement. For many repeated measurements of the same line on the standard step height (a rigid, well defined vertical step) we have found the random error from the DektakXT is on the order of ± 5 nm for the 917 nm standard and 0.05 µm for the 24.925 µm standard. The random error with the P17 profiler is even smaller.

To estimate the overall accuracy of the profiler's measurements you can convolute these various sources of error. The error sources are shown graphically in Figure 2 for measuring the small standard step with the DektakXT's smallest range. You can see an uncertainty budget for the DektakXT measurements here (made by Rebecca Ettlinger): Media:uncertainty budget Dektak rev.xlsx. It is based on the assumption that all the error sources are independent and can therefore be added by the sum of squares method.

The resulting error calculation for the DektakXT of a 1 µm very well defined standard step is about 2 % (as the uncertainty on the calibration standard dominates), while for a very well defined step of 25 µm the cumulative error is about 0.7-1 %. These are the uncertainties listed in the technical specifications for the instruments. However, in real devices the random error will often be much larger than for our standard samples and so the real confidence interval will be larger.

To improve the accuracy of your particular measurement, you should repeat the measurement several times and estimate the standard deviation. If the scatter is quite small you can calculate the error on the standard step height as a percentage of your step height and include it in a calculateion of the total error using the sum of squares method as done in the uncertainty budget above. If the scatter of your measurements is large that will probably be the dominant source of error in your measurement.