Specific Process Knowledge/Etch/KOH Etch/ProcessInfo: Difference between revisions
Appearance
| Line 61: | Line 61: | ||
==Theory== | ==Theory== | ||
===Definition of structures=== | |||
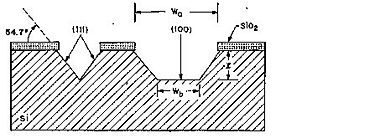
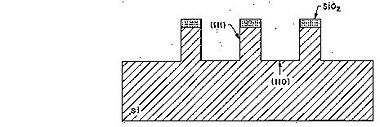
Due to the almost inert (111)-planes it is possible by KOH etching to realize high aspect ratio structures in sigle crytalline silicon using the (111)-planes as sidewalls. In Si(100) these sidewalls are inclined - 54.7<sup>o</sup> with respect to the (100) surface - whereas in Si(110) the sidewalls are vertical (see figures below). | |||
<gallery caption="Anisotropic wet silicon etch: dependency on crystal orientation" widths="380px" heights="150px" perrow="2"> | |||
Image:KOH_Anisotropy.jpg|Etched profile when etching Si(100). | |||
Image:KOH_Anisotropy(110).jpg|Etched profile when etching Si(110). | |||
</gallery> | |||
<br clear="all"/> | |||
For Si(100), the relation between the width of the bottom of the etched groove (W<sub>b</sub>) and the width of the opening (W<sub>o</sub>) at the wafer surface in a groove etched to the depth l is given by: | |||
<math>W_b = W_o - 2lcot(54.7^o) = W_o - \sqrt{2} l</math> | |||
<br clear="all" /> | |||
Revision as of 15:28, 13 March 2018
QC
Quality Control (QC) for the KOH Si etching baths.
| Quality Control (QC) for Si Etch 01, and Si Etch 02 | ||||||||||||||||||||||||||
|
Mixing KOH
Theory
Definition of structures
Due to the almost inert (111)-planes it is possible by KOH etching to realize high aspect ratio structures in sigle crytalline silicon using the (111)-planes as sidewalls. In Si(100) these sidewalls are inclined - 54.7o with respect to the (100) surface - whereas in Si(110) the sidewalls are vertical (see figures below).
- Anisotropic wet silicon etch: dependency on crystal orientation
-
Etched profile when etching Si(100).
-
Etched profile when etching Si(110).
For Si(100), the relation between the width of the bottom of the etched groove (Wb) and the width of the opening (Wo) at the wafer surface in a groove etched to the depth l is given by: