Specific Process Knowledge/Characterization/XRD/Process Info

Process information

The following types of measurement may be carried out with the Rigaku SmartLab, among others.

XRR

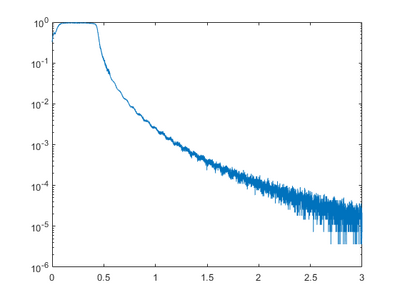
With X-Ray Reflectivity measurements, it is possible to obtain information on thickness, density, and both surface and interface roughness on thin films. The technique does not depend on crystal structure and can be used on both amorphous, poly-, and single-crystalline materials. For film thickness measurement, films op to around 100 nm can be measured. You are welcome to try it on thicker films, but please confirm the measurement the first time by use of other equipment. XRR is a special case of a Theta/2Theta measurement. Rigaku gives a good explanation of the principles behind the XRR in this paper.

Theta-2Theta

A theta-2theta scan can be used for identifying peaks and hence lattice constants and possible crystal orientations. It will also be possible to say something about the materials of the crystal, but it is not suitable for identification of composition. If a multilayers structure is, present a simulation of the stricter and comparison to the measurement can help identify layer thicknesses, atomic ratios, and interface roughness’s.

Rocking curve

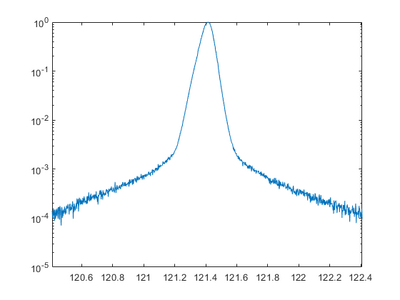
A rocking curve is measured by fixing the 2Theta angle and changing the incident angle omega, which is the same as rocking the sample in the setup. This can be used to determine the preferred orientation and the degree of orientation of the measured material. For a perfect crystal and rocking curve will show a single sharp peak, if the layers are not perfect crystalline the diffraction peak will broaden. If an epitaxial layer is grown on a preface substrate, and the sample alignment is done to the substrate peak, a shift in omega will indicate a tilt in the crystal planes. A broadening could mean a dislocations, mosaicity, or curvature of the sample.

Pole figure

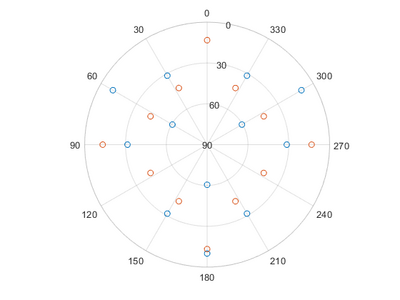
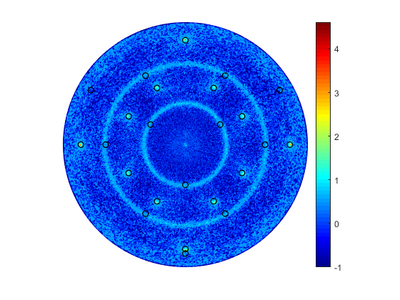
Pole figures can be used to determine the orientation of a crystal. For polycrystalline materials, it is possible to determine if there is a preferred direction of the crystal grains. In a pole figure, a measurement of a predefined peek for the material is measured in the half sphere above the sample. This will result in a map of intensities in relation to the angles from the surface normal and along sample rotation. For instance if you have a single crystalline sample with a [0 0 1] surface and measure on the [1 1 1] lattice plane, you should find 4 peaks spaced 90° in beta and at 35.26° in alpha.

Peak angles can be calculated by simple vector calculations; however, I have made a small MATLAB script calculating them for you. To use the script open MATLAB and call the program with two vectors as input. First vector should be your surface orientation, second input the plane you measure on. For a [1 1 1] substrate surface and a [3 1 1] plane and a [0 0 1] substrate surface and a [1 3 3] plane, where the measurement planes are dependent on the 2theta angle, the command looks like this:

PoleFigureAngles([1 1 1; 0 0 1],[3 1 1; 1 3 3])

It is also possible to give a path for a file exported from 3D Explore with contour data from a measurement, and a rotational correction for the data:

PoleFigureAngles([1 1 1; 0 0 1],[3 1 1; 1 3 3],'\Au_thin_inplanepole_WF1_m2.txt',30.9)

Which will give the following table and pictures, without a file input only the table and the first graph will be given:

Alpha	Beta	Alpha	Beta
10.02	60.00	13.26	0.00
10.02	300.00	13.26	270.00
10.02	180.00	13.26	90.00
31.48	30.00	13.26	180.00
31.48	330.00	43.49	333.43
31.48	90.00	43.49	296.57
31.48	270.00	43.49	26.57
31.48	150.00	43.49	243.43
31.48	210.00	43.49	63.43
60.50	60.00	43.49	206.57
60.50	300.00	43.49	116.57
60.50	180.00	43.49	153.43

Rigaku describes Pole figures this paper.